Nestle¶
/ˈnesəl/ (rhymes with “wrestle”)
Pure Python, MIT-licensed implementation of nested sampling algorithms.
Nested Sampling is a computational approach for integrating posterior probability in order to compare models in Bayesian statistics. It is similar to Markov Chain Monte Carlo (MCMC) in that it generates samples that can be used to estimate the posterior probability distribution. Unlike MCMC, the nature of the sampling also allows one to calculate the integral of the distribution. It also happens to be a pretty good method for robustly finding global maxima.
Install¶
Nestle is compatible with both Python and Python 2. It requires numpy 1.6+ and, optionally, scipy. Install with pip:
pip install nestle
For the latest development version, see http://github.com/kbarbary/nestle.
Getting started¶
The following is a simple but complete example of using Nestle to sample the parameters of a line given three data points with uncertainties:
import numpy as np
import nestle
data_x = np.array([1., 2., 3.])
data_y = np.array([1.4, 1.7, 4.1])
data_yerr = np.array([0.2, 0.15, 0.2])
# Define a likelihood function
def loglike(theta):
y = theta[1] * data_x + theta[0]
chisq = np.sum(((data_y - y) / data_yerr)**2)
return -chisq / 2.
# Define a function mapping the unit cube to the prior space.
# This function defines a flat prior in [-5., 5.) in both dimensions.
def prior_transform(x):
return 10.0 * x - 5.0
# Run nested sampling.
result = nestle.sample(loglike, prior_transform, 2)
result.logz # log evidence
result.logzerr # numerical (sampling) error on logz
result.samples # array of sample parameters
result.weights # array of weights associated with each sample
- See Examples for more detailed examples.
- See The Prior Transform for more information on the
prior_tranformfunction. - See Stopping Criterion for discussion on when the algorithm terminates.
- See the API page for detailed API documentation.
Available methods¶
The trick in nested sampling is to, at each step in the algorithm, efficiently choose a new point in parameter space drawn with uniform probability from the parameter space with likelihood greater than the current likelihood constraint. The different methods all use the current set of active points as an indicator of where the target parameter space lies, but differ in how they select new points from it.
MCMC exploration (method='classic')¶
This is close to the method described in Skilling (2004). A new point
is drawn by starting at a one of the existing active points and doing
a short MCMC walk away from the point, taking a fixed number of
steps. In the walk, a new point is accepted if it has likelihood
higher than the likelihood constraint; otherwise it is rejected. The
number of steps can be controlled with the steps parameter.
Single ellipsoid (method='single')¶
This is the method described by Mukherjee, Parkinson & Liddle (2006). Determines a single ellipsoid that bounds all active points, enlarges the ellipsoid by a user-settable factor, and selects a new point at random from within the ellipsoid. The enlargement factor is designed to ensure that the high-likelihood region is completely enclosed in the ellipsoid.
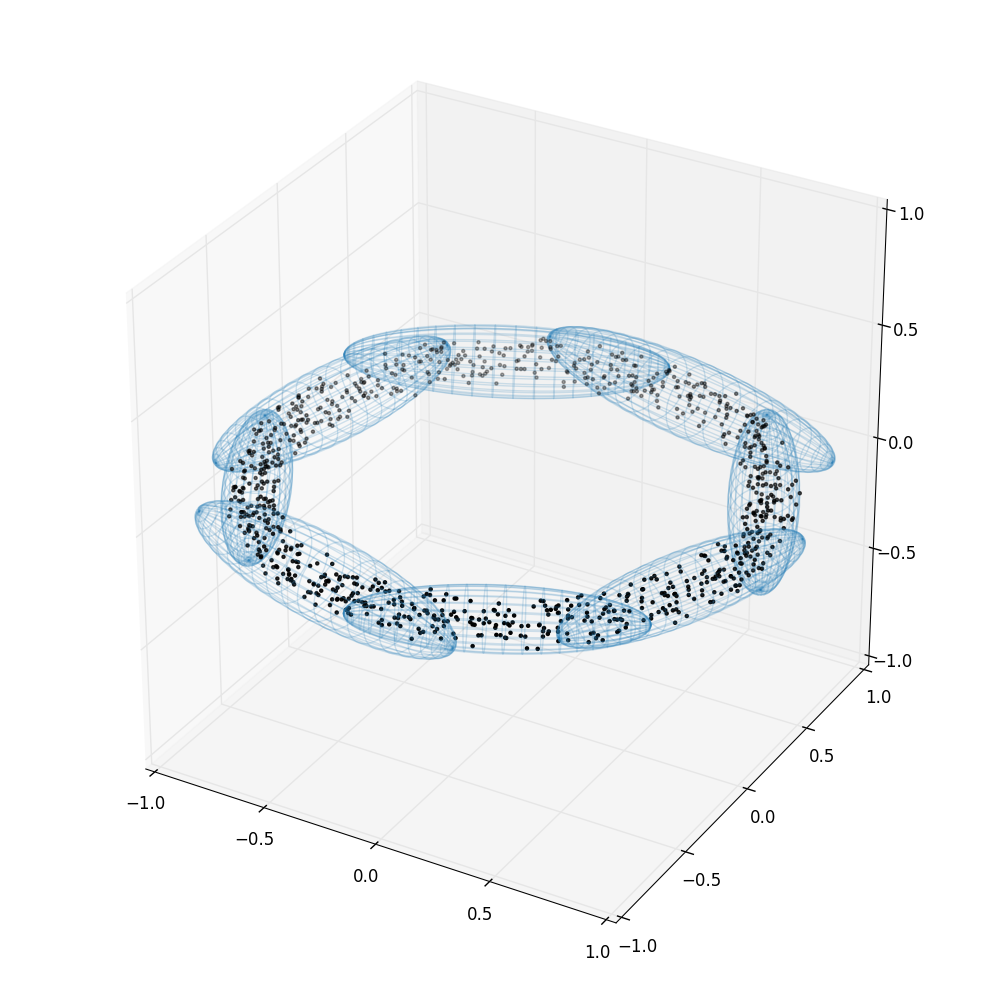
Multiple ellipsoids (method='multi')¶
This is the method first described in Shaw, Bridges & Hobson (2007) and implemented in the MultiNest software (Feroz, Hobson & Bridges 2009).
In cases where the posterior is multi-modal, the single-ellipsoid method can be extremely inefficient: In such situations, there are clusters of active points on separate high-likelihood regions separated by regions of lower likelihood. Bounding all points in a single ellipsoid means that the ellipsoid includes the lower-likelihood regions we wish to avoid sampling from.
The solution is to detect these clusters and bound them in separate ellipsoids. For this, we use a recursive process where we perform K-means clustering with K=2. If the resulting two ellipsoids have a significantly lower total volume than the parent ellipsoid (less than half), we accept the split and repeat the clustering and volume test on each of the two subset of points. This process continues recursively. Alternatively, if the total ellipse volume is significantly greater than expected (based on the expected density of points) this indicates that there may be more than two clusters and that K=2 was not an appropriate cluster division. We therefore still try to subdivide the clusters recursively. However, we still only accept the final split into N clusters if the total volume decrease is significant.
FAQ¶
What potential biases are there in these methods?
In all the nested sampling methods implemented here, there are potential biases that can affect the resulting evidence and samples. This is similar to the situation with traditional MCMC methods where one needs to be aware of potential biases such as inadequate burn-in and sample correlation. The nested sampling biases are perhaps even more nefarious as they can be more difficult to detect. They are particularly troublesome in high dimensional cases.
In the 'classic' method (MCMC exploration), the MCMC must run for
enough steps to adequately “forget” the point it started from, in
order for the final accepted point to be uniformly drawn from the
parameter space with likelihood higher than the constraint.
Particlurly for higher dimensional problems, you likely want to use a
value higher than the default of steps=20. It may be good to run
the sampling multiple times with different numbers of steps and check
that the results are consistent.
In the 'single'- and 'multi'-ellipsoid methods, we are trying
to draw an ellipsoid or ellipsoids that completely contain the
iso-likelihood region; assuming we succeed in completely containing
it, we are unbiased and the efficiency is given by the ratio of the
volume of the iso-likelihood region to the volume of the containing
ellipsoid. Unfortunately, in high dimensions the containing ellipsoid
is likely to have a far, far greater volume. This is because the
volume of a high-dimensional ellipsoid is very concentrated very
close to its surface. And this is exactly the region likely to be
within the containing ellipsoid but outside the actual iso-likelihood
region.
On the other hand there’s no guarantee that the iso-likelihood surface
is completely enclosed by the ellipsoid, and if it isn’t, the
calculated evidence will be biased. The enlarge parameter (default
1.2) enlarges the ellipsoid by some factor (default 1.2), in the hopes
that the enlarged ellipsoid completely encloses the surface. In
practice this works pretty well for up to tens of parameters. For
larger numbers of parameters, it is probably better to use the
'classic' method with a large number of steps.
So how many dimensions can my problem have?
Very roughly, the answer is “tens” and not “hundreds”. However I haven’t done any exhaustive studies of bias in high dimensions.
How many active points should I use?
It depends. The number of points primarily affects the numerical
accuracy of the results, but there are a couple other
considerations. For the ellipsoid-based methods, ndim + 1 is the
absolute minimum number of points necessary to characterize an
ellipsoid but this will give quite poor estimates. A warning is raised
if the number of points is less than 2 * ndim. Ideally you will have
at least several times more than this. For problems with just a few
parameters (<=5), I get good enough results with just 100 points. If
the posterior is likely to be multi-modal and you’re using the
'multi' method, you will want additional points in order to
characterize each mode well.
What are the differences between the ‘multi’ method and MultiNest?
First, the multi-ellipsoid method in Nestle is based on the algorithm described in Feroz, Hobson & Bridges (2009), so it doesn’t yet include any later algorithmic improvements in the MultiNest software. Second, there are subtle but important differences in the part of the algorithm that decides when to split an ellipsoid into multiple ellipsoids. I found that implementing the algorithm precisely as described gave biased results in higher dimensions due to the ellipsoids being split too aggressively into a large number of very small ellipsoids that no longer enclose the full iso-likelihood surface. Therefore, the implementation in Nestle is more conservative about splitting ellipsoids. This results in a slightly lower efficiency but greater robustness.
Sampling is taking a long time. What should I do?
First, you can check the progress by passing the parameter
callback=nestle.print_progress to see how sampling is progressing.
If you see the progress in iterations slowing down as sampling
progresses, your likelihood may be multimodal. The default method is
the single ellipsoid method ('single'). When the likelihood is
multimodal a single ellipsoid encompassing all active points will
include the “valleys” in the posterior, and sampling from the single
ellipsoid will therefore be inefficient for selecting points higher
than the likelihood constraint. In this case try method='multi'.
If sampling seems to be progressing efficiently, it might be the case that the high likelihood regions of the parameter space are very small compared to the prior volume. Nested sampling starts by uniformly sampling the entire prior volume. Then, on each iteration the volume sampled by the active points shrinks by a constant factor. Thus, the number of iterations necessary increases as the high-likelihood region becomes smaller relative to the prior volume. It is important to consider whether your priors are well-motivated and whether they might be overly conservatively wide. (Note that an overly conservative prior will also decrease the evidence!)
References¶
Feroz, Hobson & Bridges 2009. MultiNest: an efficient and robust Bayesian inference tool for cosmology and particle physics. MNRAS, 398, 1601.
Mukherjee, Parkinson & Liddle 2006. A Nested sampling algorithm for cosmological model selection. ApJ, 638, L51.
Shaw, Bridges & Hobson 2007. Efficient Bayesian inference for multimodal problems in cosmology. MNRAS, 378, 1365.
Silvia & Skilling 2006. Data Analysis: A Bayesian Tutorial, 2nd Edition. Oxford University Press.
Skilling, J. 2004. Nested Sampling. In Maximum entropy and Bayesian methods in science and engineering (ed. G. Erickson, J.T. Rychert, C.R. Smith). AIP Conf. Proc., 735, 395.
Citation¶
If you use Nestle in your work, please cite the github repository and the relevant references listed above.