Bounding Ellipsoids¶

Illustration of determining bounding ellipsoids in 3 dimensions.

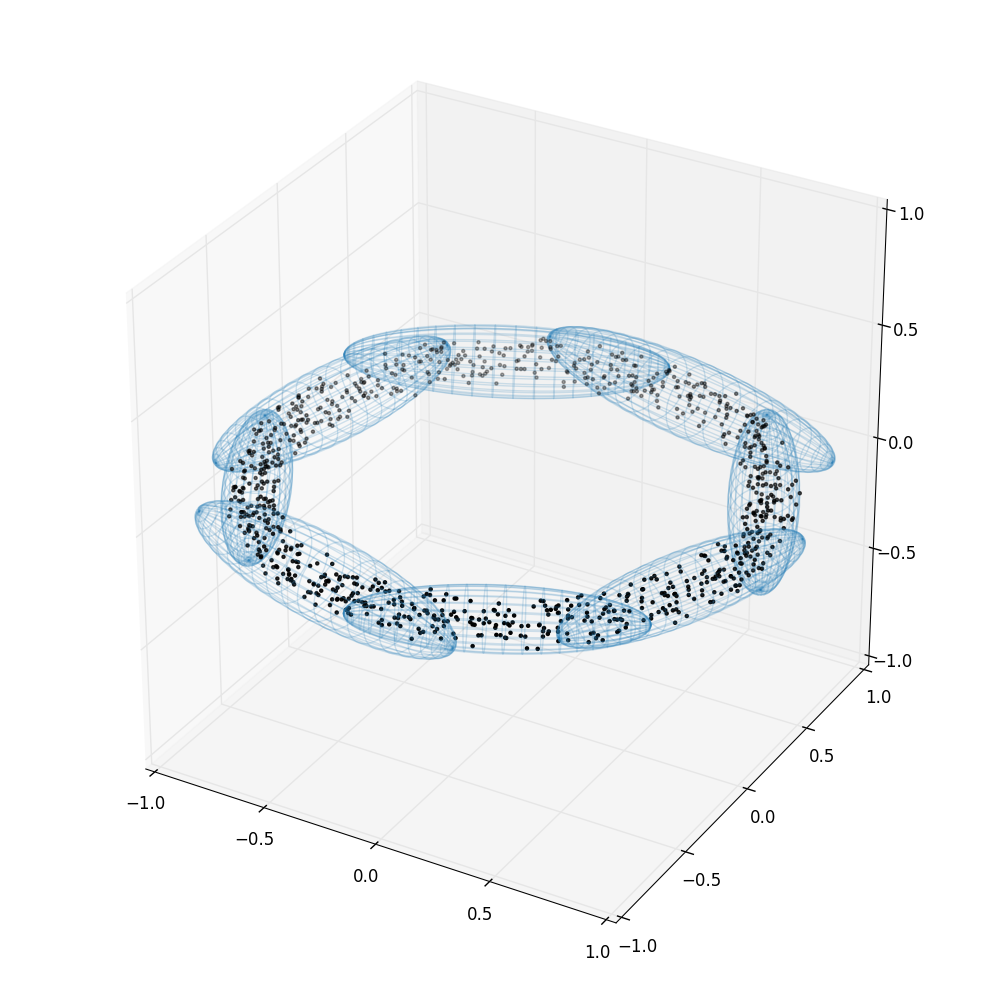
For complex iso-likelihood surfaces (ones not well-approximated by a single ellipsoid), Nestle will bound the points in multiple ellipsoids when using the 'multi' method. Here, we draw points uniformly from a torus and use Nestle to determine an optimal set of ellipses bounding the points.

import math

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

import nestle

# seed RNG for reproducible results
np.random.seed(0)


def rand_torus(ro, ri, npoints):
    """Generate points within a torus wth major radius `ro` and minor radius
    `ri` via rejection sampling"""
    out = np.empty((npoints, 3), dtype=np.float64)
    i = 0
    while i < npoints:
        # generate point within box
        x = np.random.uniform(-1., 1., size=3)
        x[0:2] *= ro + ri
        x[2] *= ri

        r = math.sqrt(x[0]**2 + x[1]**2) - ro
        if (r**2 + x[2]**2 < ri**2):
            out[i, :] = x
            i += 1

    return out


def plot_ellipsoid_3d(ell, ax):
    """Plot the 3-d Ellipsoid ell on the Axes3D ax."""

    # points on unit sphere
    u = np.linspace(0.0, 2.0 * np.pi, 100)
    v = np.linspace(0.0, np.pi, 100)
    z = np.outer(np.cos(u), np.sin(v))
    y = np.outer(np.sin(u), np.sin(v))
    x = np.outer(np.ones_like(u), np.cos(v))

    # transform points to ellipsoid
    for i in range(len(x)):
        for j in range(len(x)):
            x[i,j], y[i,j], z[i,j] = ell.ctr + np.dot(ell.axes,
                                                      [x[i,j],y[i,j],z[i,j]])

    ax.plot_wireframe(x, y, z,  rstride=4, cstride=4, color='#2980b9', alpha=0.2)


# Generate points within a torus
npoints = 1000
R = 1.0
r = 0.1
points = rand_torus(R, r, npoints)
torus_vol = 2. * math.pi**2 * R * r**2

# Determine bounding ellipsoids
pointvol = torus_vol / npoints
ells = nestle.bounding_ellipsoids(points, pointvol=pointvol)

# plot
fig = plt.figure(figsize=(10., 10.))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='k', marker='.')
for ell in ells:
    plot_ellipsoid_3d(ell, ax)

ax.set_xlim(-1., 1.)
ax.set_ylim(-1., 1.)
ax.set_zlim(-1., 1.)
ax.set_aspect('equal')
fig.tight_layout()
plt.show()

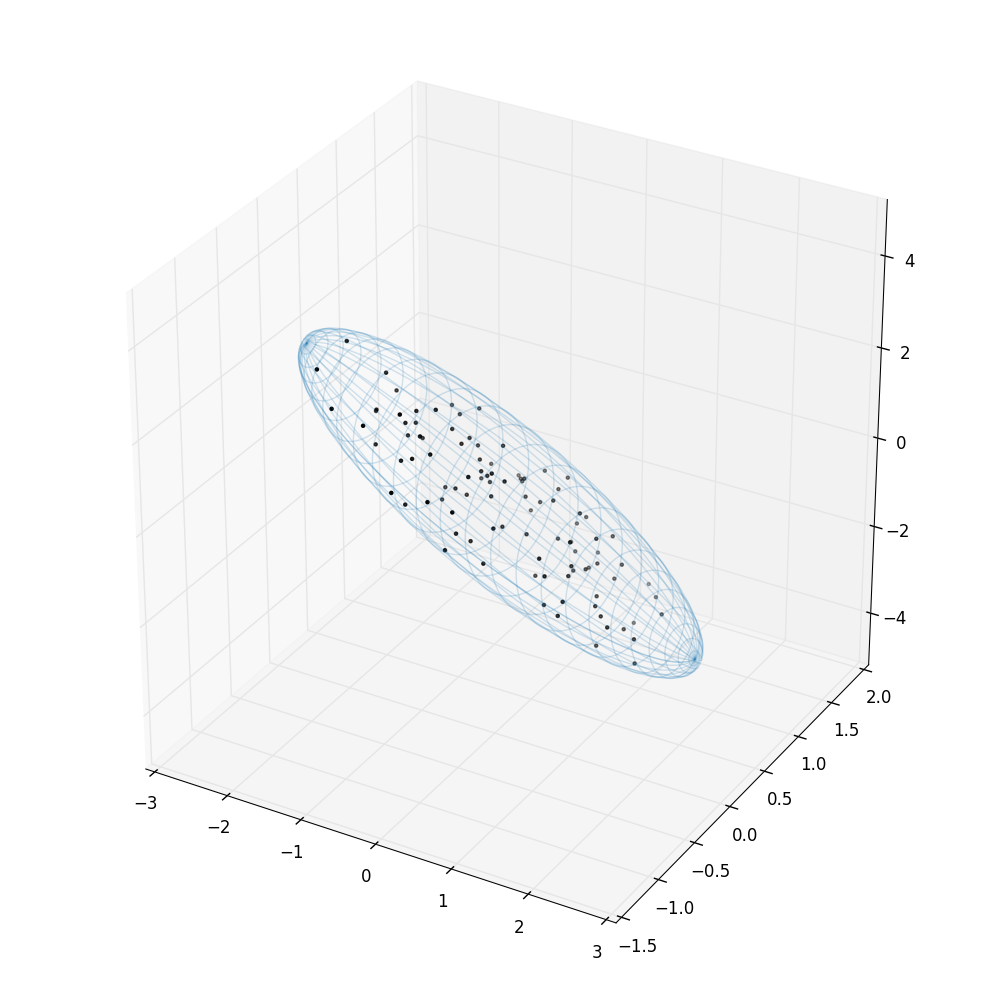
../_images/sphx_glr_plot_ellipsoids_001.png

Single ellipsoid¶

Nestle correctly identifies a cloud of points as belonging to a single ellipsoid.

# Generate samples drawn from a single ellipsoid
npoints = 100
A = np.array([[0.25, 1., 0.5],
              [1., 0.25, 0.5],
              [0.5, 1., 0.25]])
ell_gen = nestle.Ellipsoid([0., 0., 0.], np.dot(A.T, A))
points = ell_gen.samples(npoints)
pointvol = ell_gen.vol / npoints

# Find bounding ellipsoid(s)
ells = nestle.bounding_ellipsoids(points, pointvol)

# plot
fig = plt.figure(figsize=(10., 10.))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(points[:, 0], points[:, 1], points[:, 2], c='k', marker='.')
for ell in ells:
    plot_ellipsoid_3d(ell, ax)

fig.tight_layout()
plt.show()

../_images/sphx_glr_plot_ellipsoids_002.png

Total running time of the script: ( 0 minutes 0.736 seconds)

Generated by Sphinx-Gallery